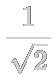
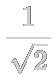
What's going on?
If you clicked that coin, you just witnessed a quantum coin flip; the most random coin flip on the internet.
What does that mean?
How do computers pick (pseudo)random numbers? While this task is seemingly simple, there’s a whole world of complexity beneath the surface. This complex stuff matters.
Computers are built on ‘bits’, or little electrical switches that can be either on or off. In a sense, computers are valuable only because they are NOT random at all. Chip processors have invested billions over decades to ensure that their bits are completely deterministic so that our cat videos will load reliably.
Take a second to think about the basic logic gates, and how you would build instructions that result in a computer returning a number randomly.
Surprisingly difficult, right? You can actually find doctorate programs1 focused solely on the mathematics of randomness!
It turns out that this problem is actually important - specifically, the ability for computers to select a random number in such a way that no human (or external computer) can predict what number will be selected. This functionality is important - for example:
Lottery drawings must be fair and unpredictable - whether the drawing is for school admittance, draft picks, or cash.
Digital gambling games must be truly random (think of a digital card deck shuffle).
Perhaps most importantly, random number generation is a crucial component of cryptography. To keep information secure, many encryption methods rely on the random generation of a numeric key, and if this key is predictable in any way, then the encryption is useless as a hacker can 'unlock' the information quite easily.
Today, computers generate random numbers in 1 of 2 ways:
For less important applications, pseudo-random numbers do just fine. This means that while the number is not truly random (and may be predictable with enough effort), it is generated from such irrelevant data that, for its purpose, it’s sufficiently arbitrary. (pick the value of the current millisecond, multiply that by X, subtract Y, divide by Z...)
For critical applications (like the ones listed above), the computer must actually use information outside of itself to “seed” random information. For example, random.org collects atmospheric data to generate random numbers. While this will feel random in any practical sense (no one can predict the next value, it’ll contain the properties of the distributions it aims to simulate), there are 2 caveats:
Even atmospheric noise has patterns, and random.org does process the raw data they collect before displaying it
From a theoretical perspective, you actually could predict atmospheric noise if you could accurately simulate the movement of molecules surrounding the sensor! This is infeasible but, again, not provably impossible, and folks have done some wild things to predict randomness when the incentives are large enough...
ENTER quantum computing.
Quantum computers are a fundamentally new form of computing information. Quantum computers use “qubits” (quantum bits) that utilize what we know of quantum mechanics to enable previously impossible calculations.
One such example is randomness - true randomness.
What happens when the coin flips?
To determine the coin flip results2, a quantum computer at IBM prepares a qubit into an evenly balanced superposition.
IBM’s quantum computers use transmon qubits, which are a type of superconducting charge qubit. Superconducting qubits are assembled from material with zero charge resistance when cooled to below 1°K, which construct an isolated “island” that can hold a pair of electrons. If a pair is present on the island, that is a logical ‘1’ for the qubit; if no pair is present, that is a logical ‘0’. Thanks to the strangeness of the quantum world, this technology can create a superposition of both states, such that an electron pair both is and is not on the island.
Upon ‘measurement’, the superposition collapses back into either a 1 or a 0 (with equal probability), but importantly, there is strong theoretical basis for believing that no one will ever be able to predict which will occur. It is, in a profound sense, harnessing the inherent randomness of the universe3 itself.
Credit: IBM newsroom
What's going on with the diagram below the coin?
This is a quantum circuit diagram, which is a way to represent a series of quantum operations that will be applied to one or more qubits (in our case, just one qubit). These are not actually physical cables through which anything is moving, but rather, an analogue to physical circuits to make it easier to conceptualize the changing qubit state. You should instead think of the movement of a qubit through the circuit as the passage of time. At the end, we measure the qubit’s state, which collapses the state if it is in a superposition.
So what's with the |0> and |1> thing?
These are the quantum basis states for a one-particle system and can be represented in what’s called bra-ket or Dirac notation as |0> and |1>. Single qubit states are represented as 2D vectors (instead of integers, as in classical computing). Mathematically, bra-ket notation is simply a shorthand way to represent a vector state of a qubit. |0> represents the state [1, 0] and |1> represents the state [0, 1]. In the context of a quantum coin flip, you can think of |0> as the “Tails” state and |1> as the “Heads” state.
And what about the ?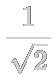
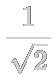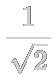This represents the amplitude that each basis state has in the state representation of a qubit. The amplitudes encode information about the probability that the qubit will be in either basis state after measurement. So when you see the qubit state shown as |0> + |1>, this means that for this qubit, the amplitude of both the |0> and the |1> basis states are 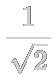. We call this a superposition of the |0> and |1> states.
For any generic qubit, a superposition can be represented by a combination of the basis states and their amplitudes as α|0> + β|1> (which is really just a different way to represent the vector [α, β]), where α is the amplitude for |0> and β is the amplitude for |1>. Upon measurement, the state collapses from a superposition into either the |0> or |1> state.
The length of a qubit’s state vector must equal 1, representing a total probability of 100%, so therefore α2 + β2 must be equal to 1. We can see this holds true for the state 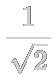|0> + 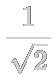|1>, where α equals 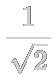and β equals 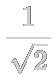, so α2 + β2 = ½ + ½ = 1. This means that 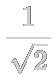|0> + 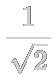|1> represents an equal probability that our qubit is in the |0> or the |1> state when measured, which is a good quantum approximation for a 50/50 coin flip!
And the H?
This is a Hadamard gate, which is a specific type of quantum logic gate. We’ll avoid going too far into the math here (if we haven’t already ☻), but its impact on a qubit in the |0> state is to create the superposition 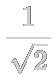|0> + 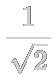|1>, or an equal chance of heads & tails, which is exactly what we need.
That's all folks!
We hope you enjoyed learning a bit about the basics of quantum computing and its applications! The problem of pseudo-random number generation remains unsolved for most applications, and yet, by clicking the above coin, you may have generated more truly random numbers than the most advanced cryptographer only a few years ago.
Learn More
Is anyone actually using Quantum Random Number Generators (QRNGs) today? Yes! For example, the latest Galaxy Smart phones now use a QRNG to ensure safer authentication and data encryption.
If you want to dive deeper into the mathematics of quantum computing, see these resources:
Some light quantum mechanics by 3Blue1Brown
Important Note: This is a purely educational site and should not be relied on for anything commercial in any way.
1 I wonder how they handle lotteries for enrollment times?
2 Yes, I acknowledge that IBM’s current machines have queue times, your results might have been pre-calculated on a quantum machine and cached, and thus, still not perfectly random/unhackable. I’m making a point and a fun toy, not defending my dissertation here.
3 Much to the chagrin of Everett and Deutsch, we will assume there’s only one universe when the coin flips.